CG2 - 3D 空间的点线面

05 Jul 2015

0、概述

在 2D/3D 空间中的点、线、面都具有其通用含义：

在 3D 图形编程中，“向量”也是一个极其重要的数据结构，用于表示一条有向线段，由不同方向的分量组成。

在我的实现中，Point 和 Vector 使用同一个数据结构，通过 typedef 声明成别名。现在回想起来，这绝对是一个糟糕的决定。不仅结构体存在二义性，而且对调用这两个结构的函数也埋下了隐患。请各位引以为戒。

点线面的坐标计算并不复杂，但细节颇多，《大师技巧》和其他图形学的书中都有详实的描述，在此不讲述具体实现，而着重描述数学运算符与我的渲染器中 API/运算符 的对应关系。

点与向量的实现在 Vector.h 中，线和面的实现在 LMath.h 中。

1、点

此处说的点就是向量的意思，几乎所有的计算都是对向量有意义的，对于点只有 +、-、* 有意义，所以说我的实现中为了节省这几行代码带来的二义性是不值得的，将在下一重构时修复这个问题。

$$ \begin{array} {rl} Operator & API \\ \hline |\vec{u}| & \vec{u}.length() \\ -\vec{u} & \vec{u}.reverse() \\ \frac{\vec{u}}{|\vec{u}|} & \vec{u}.normalize() \\ \vec{u}\bullet\vec{v} & \vec{u}.dot(\vec{v}) \\ \frac{\vec{u}\bullet\vec{v}}{|\vec{u}|*|\vec{v}|} & \vec{u}.cos(\vec{v}) \\ \vec{u}+\vec{v} & \begin{cases} \vec{u}.operator+(\vec{v}) \\ \vec{u}.operator+=(\vec{v}) \end{cases} \\ \vec{u}-\vec{v} & \begin{cases} \vec{u}.operator-(\vec{v}) \\ \vec{u}.operator-=(\vec{v}) \end{cases} \\ \vec{u}*\vec{v} & \begin{cases} \vec{u}.operator*(\vec{v}) \\ \vec{u}.operator*=(\vec{v}) \end{cases} \\ \vec{u}\times\vec{v} & \vec{u}.cross(\vec{v}) \\ \end{array} $$

此处对用 operator 运算符做了两种处理：产生临时变量返回、改变本身属性。

做这两种区分主要出于以下考虑：1）直接运算时，往往并不希望改变变量本身的参数，而仅仅是希望获得返回值；2）当执行运算赋值时，则确定将会改变变量本身的参数，所以在不产生错误的情况下可以修改原始参数。

1
2
3
4
5
6
7
8
9
10
11
12
inline Vector3D Vector3D::operator+(const Vector3D& v)
{
    Vector3D tmp;
    tmp.x = x + v.x; tmp.y = y + v.y; tmp.z = z + v.z;
    return tmp;
}

inline Vector3D& Vector3D::operator+=(const Vector3D& v) 
{ 
    x += v.x; y += v.y; z += v.z; 
    return *this; 
}

2、线

线由起点坐标、终点坐标和由起点指向终点的向量组成，无需赘述。

3、面

3D 空间中的坐标系有两种基本的组织方式：柱面坐标系和球面坐标系。综合运用这两种坐标系，可以有效简化坐标计算。

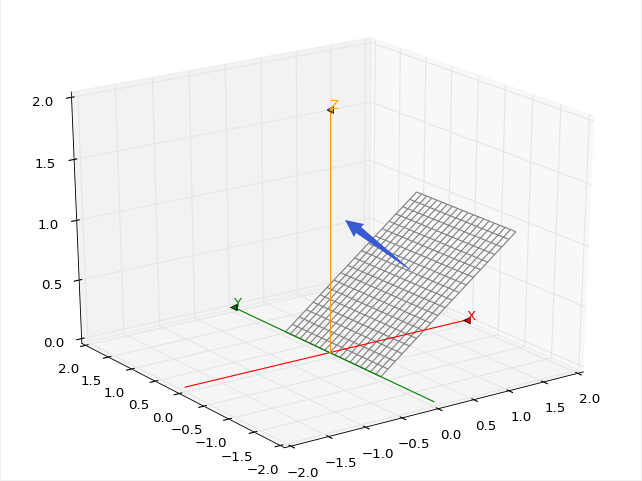
1）空间中的一个平面由平面上的一个点和平面法向量表示。

plane

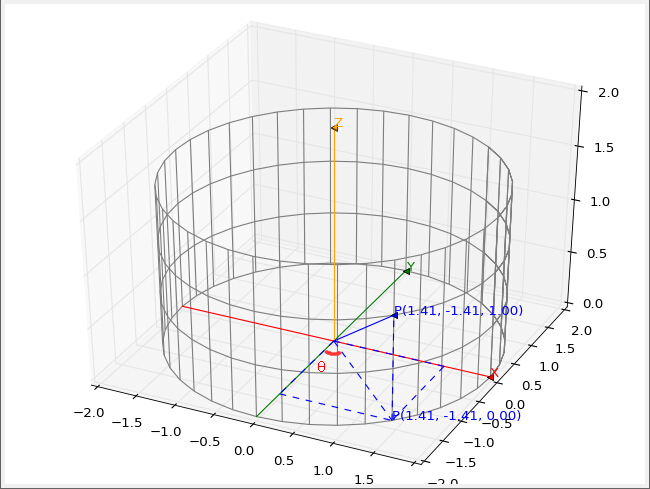
2）柱面坐标系

柱面坐标系在 2D 空间的极坐标系基础上增加了 z 轴，实现并不复杂，通常表示为：

$$ \begin{array} {} P(\rho, \theta, z) & \begin{cases} x = r * \cos(\theta) \\ y = r * \sin(\theta) \\ z = z \end{cases} \end{array} $$

spherical

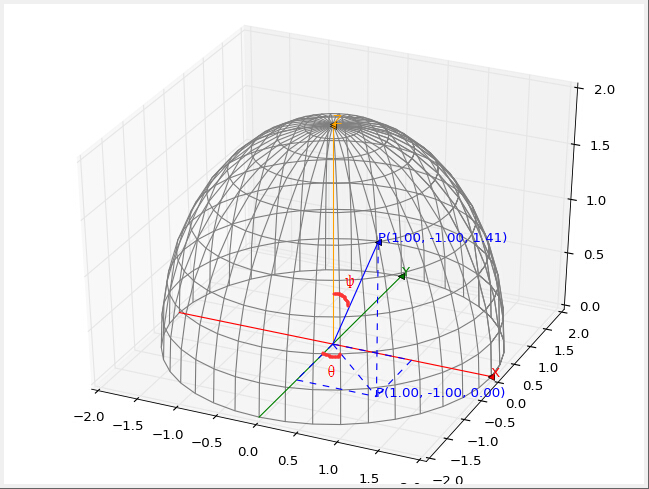
3）球面坐标系

球面坐标系中定义一个点，需要两个角度和到原点的距离。

$$ \begin{array} {} P(\rho, \phi, \theta) & \begin{cases} x = r * \cos(\theta) = \rho * \sin(\phi) * \cos(\theta) \\ y = r * \sin(\theta) = \rho * \cos(\phi) * \sin(\theta) \\ z = \rho * \cos(\phi) \end{cases} \end{array} $$

cylindrical

想要在室内给物体拍出好的照片，需要搭建一个，坐标系就是 3D 空间物体的摄影棚。有了坐标系，就可以接着把物体数据化填充到坐标系中。以上图片均使用 python + matplotlib 生成，代码在此。

这一部分我并没有讲述特别多的 3D 数学计算，如果需要深入了解，请查阅相关资料。

如果你发现我文章中的问题或希望与我交流，可以给我发邮件：plinux@qq.com。

如果你读后有些许收获，也可以到我的 Github 点赞支持。

© 2015 plinx